Update: On Monday, April 4, I will give an online talk on those results at the UC Berkeley Probabilistic Operator Algebra Seminar.
I have just uploaded the joint paper A dual and conjugate system for q-Gaussians for all q with Akihiro Miyagawa to the arXiv. There we report some new results concerning the q-Gaussian operators and von Neumann algebras. The interesting issue is that we can prove quite a few properties in a uniform way for all q in the open interval -1<q<1.
The canonical commutation and anti-commutation relations are fundamental relations describing bosons and fermions, respectively. In 1991, Marek Bożejko and I considered an interpolation between those bosonic and fermionic relations, depending on a parameter q with  (where q=1 corresponds to the bosonic case and q=-1 to the fermionic case):
(where q=1 corresponds to the bosonic case and q=-1 to the fermionic case):  . These relations can be represented by creation and annihilation operators on a q-deformed Fock space. (Showing that the q-deformed inner product which makes
. These relations can be represented by creation and annihilation operators on a q-deformed Fock space. (Showing that the q-deformed inner product which makes 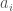 and
and 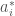 adjoints of each other is indeed an inner product, i.e. positive, was one of the main results in my paper with Marek.) In the paper with Akihiro we consider only the case where the number d of indices is finite.
adjoints of each other is indeed an inner product, i.e. positive, was one of the main results in my paper with Marek.) In the paper with Akihiro we consider only the case where the number d of indices is finite.
Since then studying the q-Gaussians 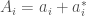 has attracted quite some interest. Especially, the q-Gaussian von Neumann algebras, i.e., the von Neumann algebras generated by the
has attracted quite some interest. Especially, the q-Gaussian von Neumann algebras, i.e., the von Neumann algebras generated by the 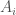 , have been studied for many years. One of the basic questions is whether and how those algebras depend on q. The extreme cases q=1 (bosonic) and q=-1 (fermionic) are easy to understand and they are in any case different from the other q in the open interval -1<q<1. The central case q=0 is generated by free semicircular elements and free probability tools give then easily that this case is isomorphic to the free group factor.
, have been studied for many years. One of the basic questions is whether and how those algebras depend on q. The extreme cases q=1 (bosonic) and q=-1 (fermionic) are easy to understand and they are in any case different from the other q in the open interval -1<q<1. The central case q=0 is generated by free semicircular elements and free probability tools give then easily that this case is isomorphic to the free group factor.
So the main question is whether the q-Gaussian algebras are, for -1<q<1, isomorphic to the free group factor. Over the years it has been shown that these algebras share many properties with the free group factors. For instance, for all -1<q<1 the q-Gaussian algebras are II1-factors, non-injective, prime, and have strong solidity. A partial answer to the isomorphism problem was achieved in the breakthrough paper by Guionnet and Shlyakhtenko, who proved that the q-Gaussian algebras are isomorphic to the free group factors for small |q| (where the size of the interval depends on d and goes to zero for  ). However, it is still open whether this is true for all -1<q<1.
). However, it is still open whether this is true for all -1<q<1.
In our new paper, we compute a dual system and from this also a conjugate system for q-Gaussians. These notions were introduced by Voiculescu in the context of free entropy and have turned out to carry important information about distributional properties of the considered operators and to have many implications for the generated von Neumann algebras.
Our approach starts from finding a concrete formula for dual systems; those are operators whose commutators with q-Gaussians are exactly the orthogonal projection onto the vacuum vector. If we also normalize such dual operators by requiring that they vanish on the vacuum vector, then the commutator relation gives a recursion, which can be solved in terms of a precise combinatorial formula involving partitions and their number of crossings, where the latter has, however, to be counted in a specific, and different from the usual, way. The main work consists then in showing that the dual operators given in this way have indeed the vacuum vector in the domain of their adjoints. The action of the adjoints of the dual operators on the vacuum gives then, by general results going back to Voiculescu and Shlyakhtenko, the conjugate variables.
One should note that whereas the action of the dual operators on elements in the m-particle space is given by finite sums, going over to the adjoint results, even for their action on the vacuum, necessarily in non-finite sums, i.e., power series expansions. Thus it is crucial to control the convergence of such series in order to get the existence of the conjugate variables. There have been results before on the existence of conjugate variables for the q-Gaussians, by Dabrowski, but those relied on power series expansions which involved coefficients of the form 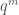 for elements in the m-particle space and thus guaranteed convergence only for small q. In contrast, the precise combinatorial formulas in our work lead to power series expansions which involve coefficients of the form
for elements in the m-particle space and thus guaranteed convergence only for small q. In contrast, the precise combinatorial formulas in our work lead to power series expansions which involve coefficients of the form  . This quadratic form of the exponent is in the end responsible for the fact that our power series expansions converge for all q in the interval (-1,1).
. This quadratic form of the exponent is in the end responsible for the fact that our power series expansions converge for all q in the interval (-1,1).
The existence of conjugate systems for all q with -1<q<1 has then, by previous general results, many consequences for all such q (some of them had been known only for the restricted interval of q, some of them for all q, by other methods). We can actually improve on the existence of the conjugate system and show that it satisfies a stronger condition, known as Lipschitz property. This implies then, by general results of Dabrowski, the maximality of the micro-states free entropy dimension of the q-Gaussian operators in the whole interval (-1,1).
Unfortunately, we are not able to use our results for adding anything to the isomorphism problem. However, the fact that the free entropy dimension is maximal for all q in the whole interval is another strong indication that they might all be isomorphic to the free group factor.
