Tag Archives: Gaussian equivalence principle

Understanding Non-Linearity in Random Matrices

Leave a reply

Update: I will give an online talk on my work with Alex in Voiculescu’s Probabilistic Operator Algebra Seminar on Monday, Feb 3, at 9am Pacific time (which is 6pm German time). In order to get the online link for the talk you should write to jgarzav at caltech dot edu.

In the post “Structured random matrices and cyclic cumulants: A free probability approach” by Bernard and Hruza I mentioned the problem about the effect of non-linear functions on random matrices and showed some plots from my ongoing joint work with Alexander Wendel. Finally, a few days ago, we uploaded the preprint to the arXiv.

What is this about? Consider a random matrix ensemble XN which has a limiting eigenvalue distribution for N going to infinity. In the machine learning context applying non-linear functions to the entries of such matrices plays a prominent role and the question arises: what is the asymptotic effect of this operation. There are a couple of results in this direction; see, in particular, the paper by Pennington and Worah and the one of Peche. However, it seems that they deal with quite special choices for XN, like a product of two independent Wishart matrices. In those cases the asymptotic effect of applying the non-linearity is the same as taking a linear combination of the XN with an independent Gaussian matrix. The coefficients in this linear combination depend only on a few quantities calculated from the non-linear function. Such statements are often known as Gaussian equivalence principle.

Our main contribution is that this kind of result is also true much more generally, namely for the class of rotationally invariant matrices. The rotational invariance is kind of the underlying reason for the specific form of the result. Roughly, the effect of the non-linearity is a small deformation of the rotational invariance, so that the resulting random matrix ensemble still exhibits the main features of rotational invariance. This provides precise enough information to control the limiting eigenvalue distribution.

We consider the real symmetric case, that is, symmetric orthogonally invariant random matrices. Similar results hold for selfadjoint unitarily invariant random matrices, or also for corresponding random matrices without selfadjointness conditions.

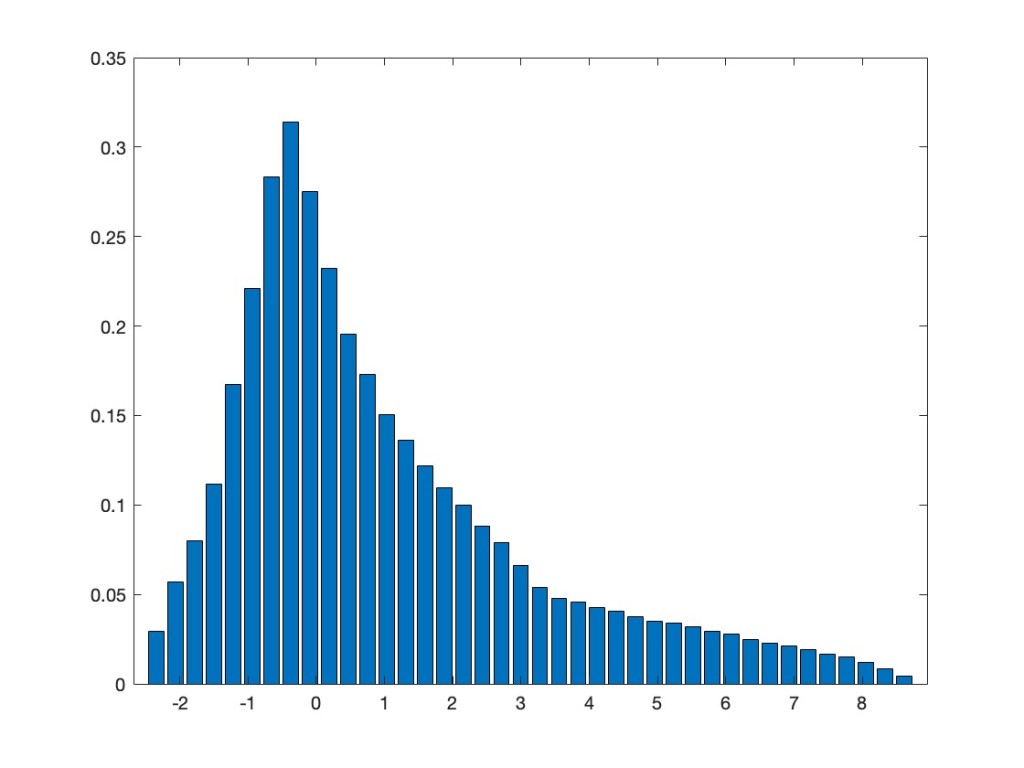
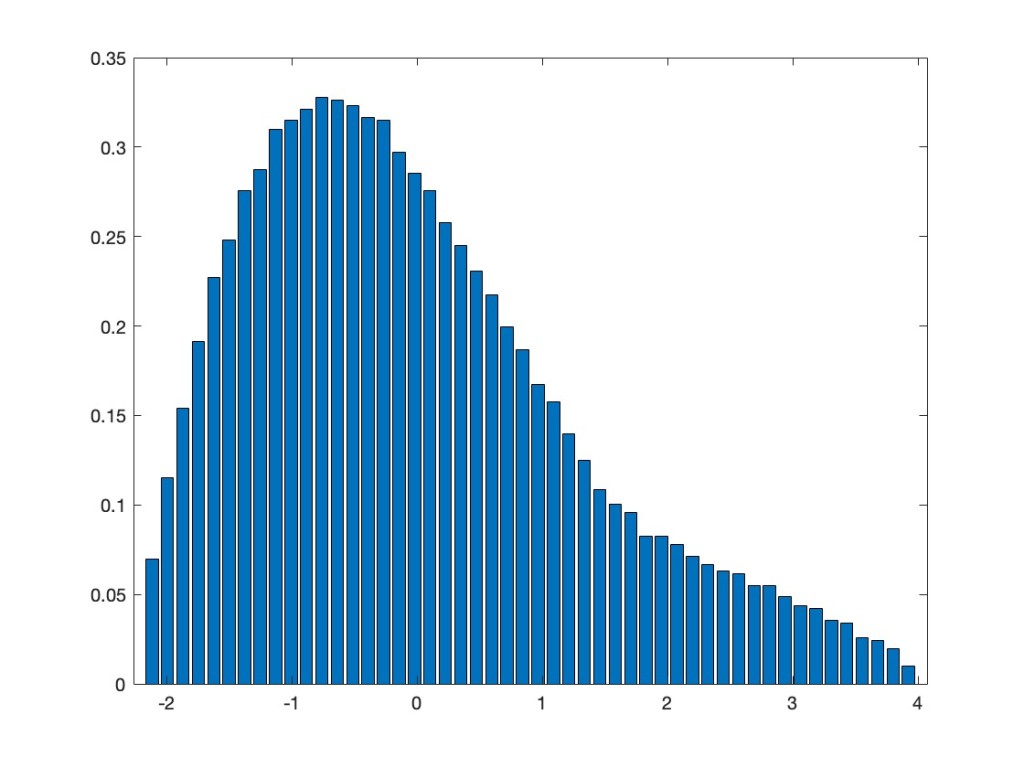
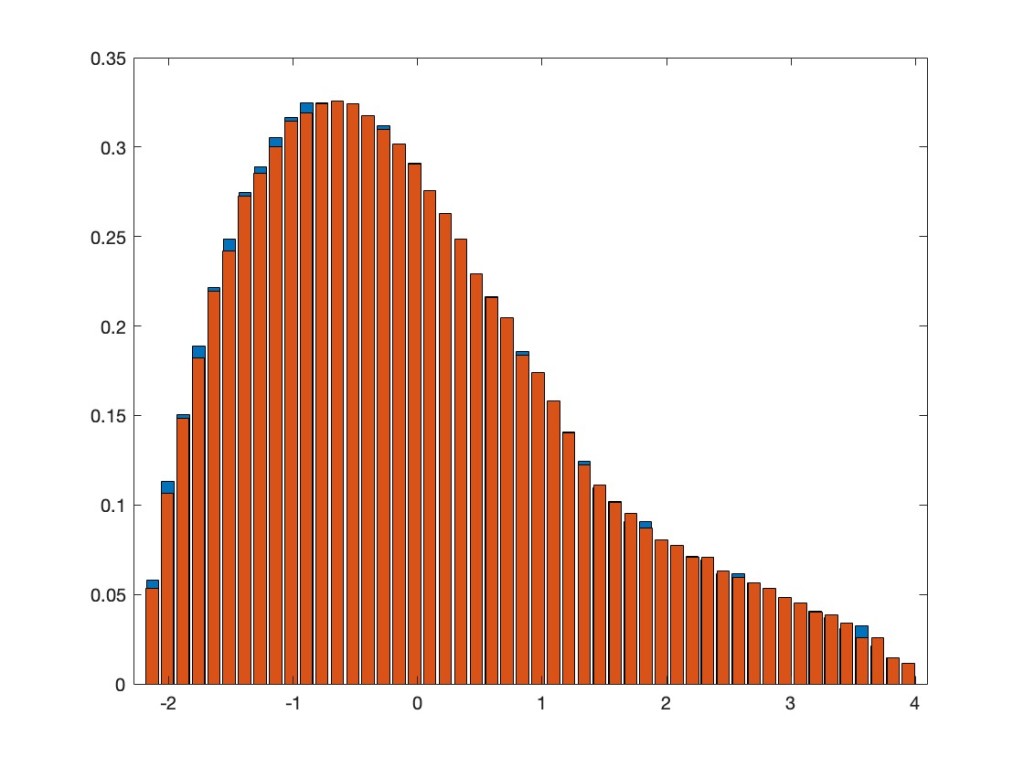
In addition to what I already showed in the above mentioned previous post, we extended the results now also to a multi-variate setting. This means we can also take, again entrywise, a non-linear function of several jointly orthogonally invariant random matrices. The asymptotic eigenvalue distribution after applying such a function is the same as for a linear combination of the involved random matrices and an additional independent GOE. As an example, take the two random matrices XN=AN2– BN and YN=AN4+CNAN+ANCN, where AN, BN, CN are independent GOEs. Note that, by the appearance of AN in both of them, they are not independent, but have a correlation. Nevertheless, they are jointly orthogonally invariant — that is, the joint distribution of all their entries does not change if we conjugate both of them by the same orthogonal matrix. We consider now the non-linear random matrix max(XN,YN), where we take entrywise the maximum of the corresponding entries in XN and YN. Our results say that asymptotically this should have the same eigenvalue distribution as the linear model aXN+ bYN + cZN, where ZN is an additional GOE, which is independent from AN, BN, CN, and where a, b, c are explicitly known numbers. The next plot superimposes the two eigenvalue distributions.

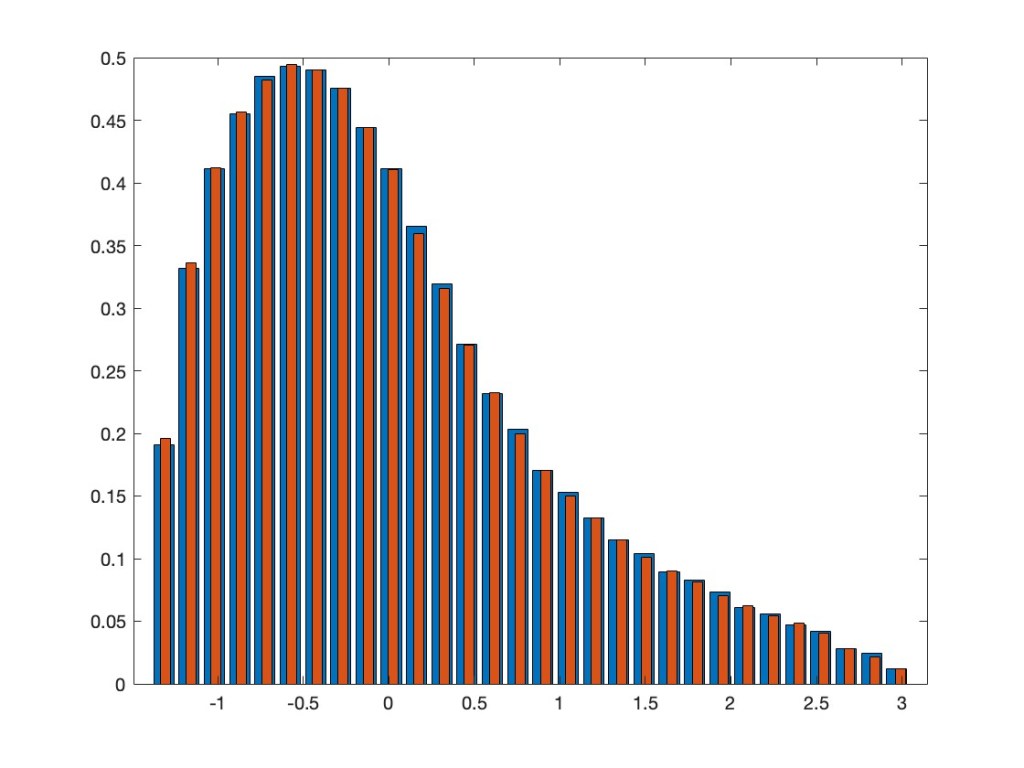
If you want to know more, in particular, why this is true and how the coefficients in the linear model are determined in terms of the non-linear function, see our preprint Entrywise application of non-linear functions on orthogonally invariant random matrices.

“Structured random matrices and cyclic cumulants: A free probability approach” by Bernard and Hruza

2 Replies

The evolution of some papers of Bernard and Hruza in the context of “Quantum Symmetric Simple Exclusion Process” (QSSEP) have been addressed before in some posts, here and here. Now there is a new version of the latest preprint, with the more precise title “Structured random matrices and cyclic cumulants : A free probability approach“. I think the connection of the considered class of random matrices with our free probability tools (in particular, the operator-valued ones) is getting nicer and nicer. One of the new additions in this version is the proof that applying non-linear functions entrywise to the matrices (as is usually done in the machine learning context) does not lead out of this class and one can actually describe the effect of such an application.

I consider all this as a very interesting new development which connects to many things, and I will try to describe this a bit more concretely in the following.

For the usual unitarily invariant matrix ensembles we know that the main information about the entries which contributes in the limit to the calculation of the matrix distribution are the cyclic classical cumulants (or ”loop expectation values”). Those are cumulants of the entries with cyclic index structure c(x_{i_1,i_2},x_{i_2,i_3},\dots,x_{i_n,i_1}) – and, for the unitarily invariant ensembles, the asymptotics of those cumulants does not depend on the chosen indices i_1,i_2,\dots,i_n. Actually, in the limit, with the right scaling, those give the free cumulants \kappa_n of our limiting matrix distribution. The idea of Bernard and Hruza is now to extend this to an inhomogeneous setting, where the indices matter and thus the limiting information is given by ”local” free cumulants \kappa_n(t_1,\dots,t_n) where the t_k are the limits of i_k/N. For the operator-valued aficionado this has the flavor of operator-valued cumulants (over the diagonals), and this is indeed the case, as shown in the paper. For the case of inhomogeneous Gaussian matrices, where the limits are given by operator-valued semicircular elements, such results are not new, going back to the work of Dima Shlyakhtenko on band matrices, and constitute one of our most beloved indications for the power of operator-valued free probability. The paper of Bernard and Hruza goes much beyond the semicircular case and opens a very interesting direction. The fact that this is motivated by problems in statistical physics makes this even more exciting. Of course, there are many questions arising from this, on which we should follow up. In particular, is there a good version of this not only over diagonal matrices; or, is there a relation with the notion of R-cyclic distributions, which I introduced with Andu and Dima a while ago in this paper?

As I mentioned at the beginning I am also intrigued by the effect of applying non-linear functions to the entries of our matrices. This is something, we usually don’t do in ”classical” random matrix theory, but which has become quite popular in recent years in the machine learning context. There are statements which go under the name of Gaussian equivalence principle, which say that the effect of the non-linearity is in many cases the same as adding an independent Gaussian random noise. Actually, this is usually done for special random matrices, like products of Wishart matrices. However, this seems to be true more general; I was convinced that this is valid for unitarily invariant matrices, but the paper of Bernard and Hruza shows that even in their more general setting one has results of this type.

In order to give a concrete feeling of what I am talking about here, let me give a concrete numerical example for the unitarily invariant case. Actually, I prefer her the real setting, i.e., orthogonal invariant matrices. For me canonical examples of those are given by polynomials in independent GOE, so let us consider here X_N=A_N^2+A_N+B_NA_N+A_NB_N+B_N, where A_N and B_N are independent GOE. The following plot shows the histogram of the eigenvalues of one realization of X_N for $N=5000$.

We apply now a non-linear function to the entries of X_N. Actually, one has to be a bit careful about what this means; in particular, one needs a good scaling and should not act naively on the diagonals, as this would otherwise dominate everything. Here is the precise definition of the entries of the new matrix Y_N.

y_{ij}=\begin{cases} \frac 1{\sqrt{N}} f(\sqrt{N} x_{ij}), & i\not=j\\ 0,& i=j.\end{cases}

For the function f, let’s take the machine learning favorite, namely the ReLU function, i.e., f(x)=\text{ReLU}(x):=\max(0,x). Here is the histogram of the eigenvalues of the corresponding matrix Y_N

But now the Gaussian equivalence principle says that this Y_N should asymptotically have the same distribution as the original matrix perturbed by a noise, i.e., as \theta_1 X_N+\theta_2 Z_N, where Z_N is a GOE matrix, independent from X_N, and where in our case \theta_1=1/2 and \theta_2=\sqrt{5(1-2/\pi)}/2. The following plot superimposes the eigenvalue distribution of \theta_1 X_N+\theta_2 Z_N to the preceding plot for Y_N. Looks convincing, doesn’t it.

One should note that the ReLU functions does not fall into the class of (polynomial or analytic) functions, for which the results are usually proved, but ReLU is explicit enough, so that probably one could also do this more directly in this case. Anyhow, all this should just be an appetizer, there is still quite a bit to formulate and prove in this direction, but I am looking forward to a formidable feast in the end.